随机数生成算法
🚲 🚗 ✈️ 🚀
🚀 较为真实的随机数获取
一个随机数需要满足以下特点:
1、在规定的数值范围内,每个数值出现的概率相同,经过一定次数的生成之后可以覆盖该范围内的所有值。
2、不能通过任何算法推导出下一个数字。
由于上述第二个条件的限制,真正的随机数是不能通过算法生成的。一般可以用硬件信息来获取,例如:
1、定时器的值。
2、获取ADC采样的值。
3、加速度传感器的值。
不过由于这些数值短时间内的变化不是很大,因此不能在短时间内连续获取。
🚀 伪随机数算法
一个良好的随机数发生器应当具备以下几个特性:
1、产生的随机数要具有均匀总体随机样本的统计性质,如分布的均匀性,抽样的随机性,数列间的独立性等。
2、产生的数列要有足够长的周期,以满足模拟计算的需要。
3、产生数列的速度要快,占用计算机的内存少,具有完全可重复性。
✈️ 线性同余法(LCG)
线性同余法是目前应用最广泛的方法之一,很多编程语言的随机数生成 API 也有采用这种方法,它利用数论中的同余运算来产生随机数,所以称为同余发生器,一般递推公式为:
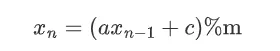
其中 a、c、m 都是常数,$x_n$ 是产生的随机数序列。即用上一个随机数 x~n-1~ 根据公式计算出随机数 x~n~,一开始时要给个初值 x~0~,也叫随机数种子。因为后面加了个取余 m 的运算,所以产生的随机数范围是 0 到 m。C语言的 rand() 函数也采用了这种方法,如下:
1 | static unsigned long int next = 1; |
可调整 a、c 的值来改变随机数的均匀性,当 a = 9,c = 7 效果较为理想。
下面是用来验证此算法的 python 程序:
1 | import matplotlib.pyplot as plt |
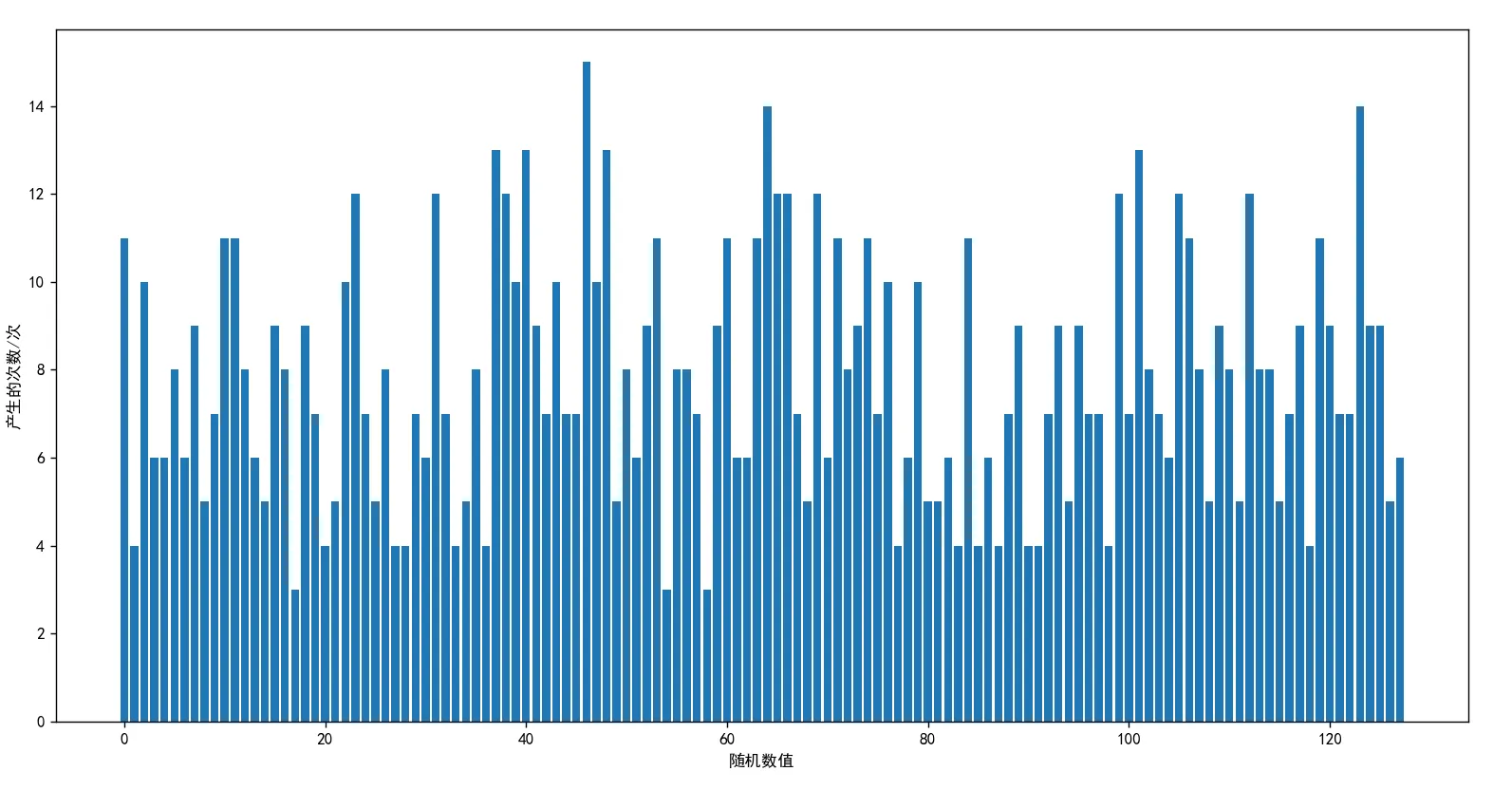
当测试次数为1000 时,生成的图片如下图所示:
当测试次数为10000 时,生成的图片如下图所示:
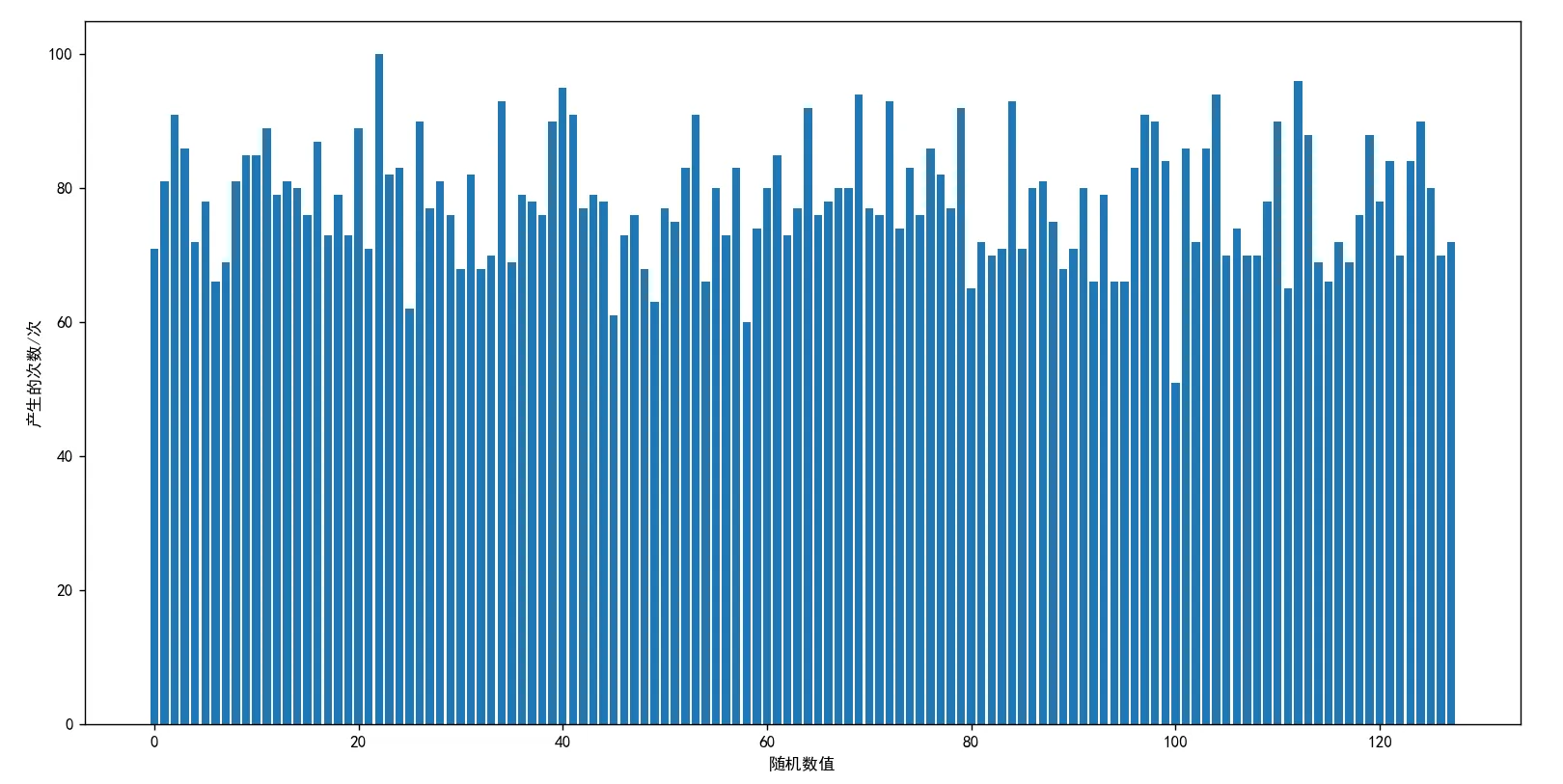
由上面两图分析可得:此算法算出来的随机数具有均匀总体随机样本的统计性质,主要优点有:
1、算法简单,占用内存小,运算量小。
主要缺点有:
1、此伪随机序列具有周期性,建议每间隔一段时间就改变一次随机种子的值。
2、各个数字出现的概率相差较大。
3、算法简单,容易被反推出 a 和 c 的值,进而被破解算出下一个“随机数”。
因此,线性同余法算法适用于对系统实时性要求高,算力较低,要求不严格的场合。可以将定时器值或其他硬件数值作为随机种子,提高数值的随机性。
且经本人测试,去掉 “>> 16” 这条语句之后,各随机数出现概率就完全一致了,不过这有利有弊,只适用于生成不会重复的数列,例如随机翻转一段内存中的随机几个 bit。
✈️ 反馈位移寄存器法(FSR)
反馈位移寄存器法通过对寄存器进行位移,直接在存储单元中形成随机数,速度很快,因此很多MCU主控里集成的随机数模块都采用了类似的方法。
python测试程序:
1 | import matplotlib.pyplot as plt |
当 wTestNum = 1000 时,生成的图片如下图所示:
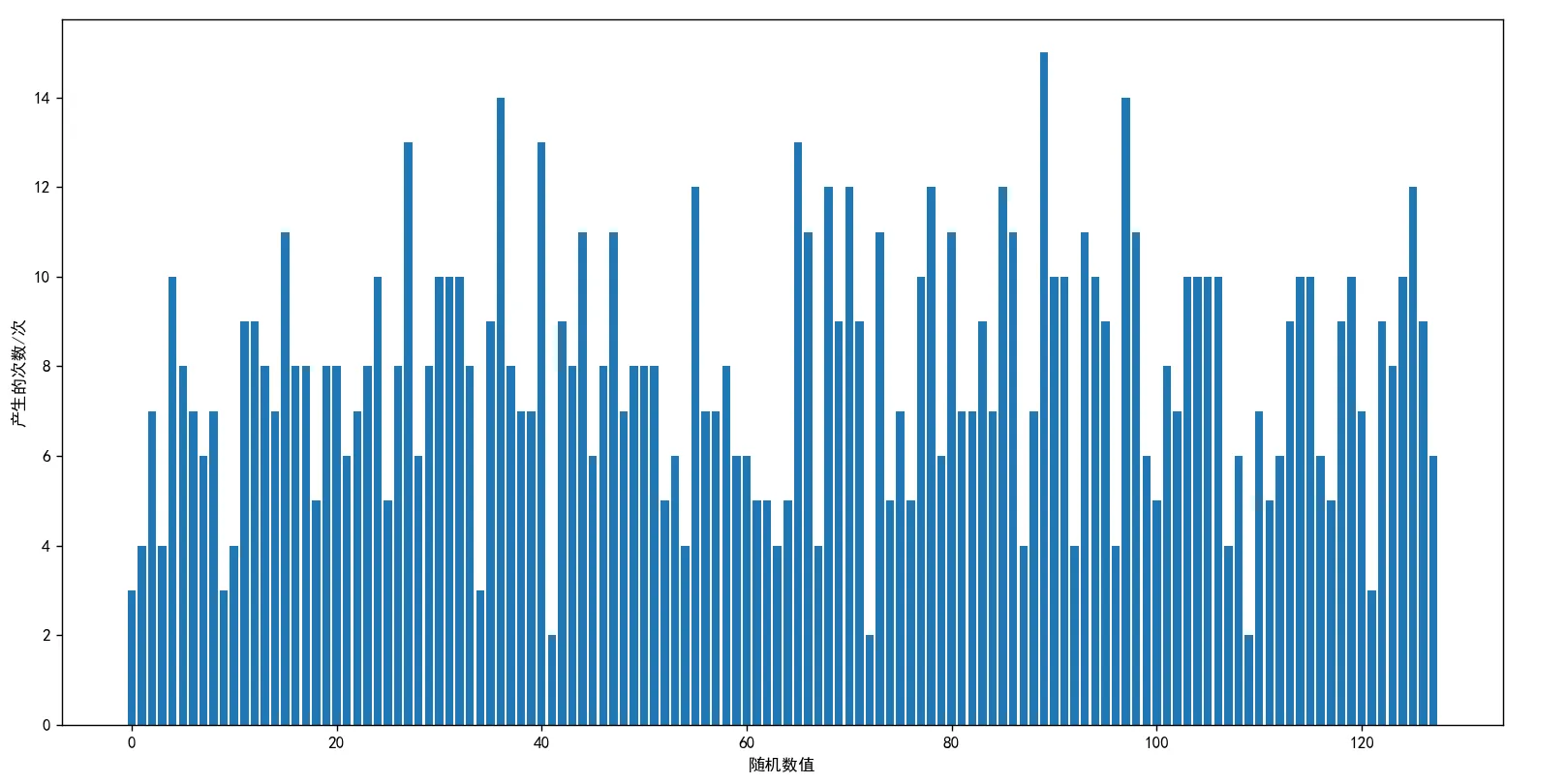
当 wTestNum = 10000 时,生成的图片如下图所示:
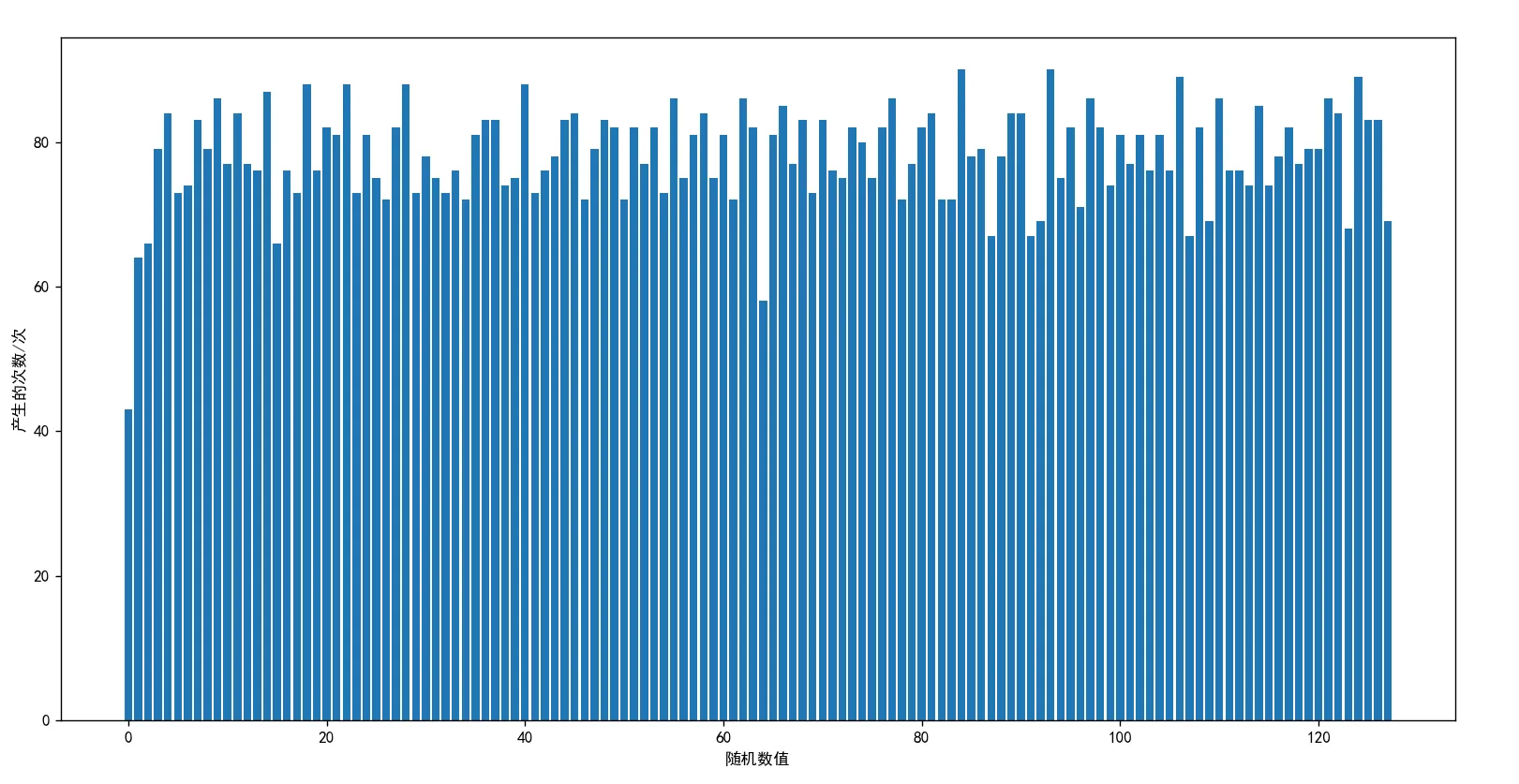
综上所述,反馈位移寄存器法具有以下优点:
1、反馈位移寄存器法可以通过对寄存器进行位移,直接在存储单元中形成随机数,速度很快,因此很多MCU主控里集成的随机数模块都采用了此方法。
缺点是:
1、如果靠软件生成会比较慢。
✈️ 组合随机数发生器
将不同的随机数发生器进行级联组合,用一种随机数发生器产生的随机数作为下一个随机数发生器的种子或者用来扰乱另一个随机数发生器,以此来获得比单一随机数发生器更好的效果。例如两个线性同余发生器进行组合,第一个随机数发生器产生随机数作为下一个发生器的c参数来对下一个随机数发生器进行扰动,以获得比单一随机数发生器更长的随机数周期。
🚀 参考资料
- 随机数生成方法及其应用:https://blog.csdn.net/qq_34254642/article/details/104011261
一种基于线性反馈位移寄存器的随机数生成方法:https://blog.csdn.net/qq_34254642/article/details/106819635
如何生成随机数+原理详细分析:https://blog.csdn.net/chenlong_cxy/article/details/112862909







